Mountain Range

Two possible distributions of heights consistent with example $1$.

Torunn lives in a mountainous residential area consisting of an $n \times m$ grid with one plot in each cell. Torunn lives in the cell at the top-left corner of the grid. Unfortunately, a particularly troublesome tenant has recently moved in, so Torunn has decided to sell her property and move elsewhere. However, she first needs to find out how much her property is worth.

Each cell in the grid has a height. All heights are unique, so for simplicity, let’s assume the heights are $1, 2, 3, \dots , n \cdot m$. Plots with higher heights are worth more on the housing market, so Torunn wants to determine the height of her plot. She has therefore gone around to each cell in the grid and checked how many adjacent cells have lower heights. A cell is considered adjacent if it shares a side (cells not on the edge of the grid have $4$ adjacent cells).

Write a program that, given the information Torunn collected, finds the minimum and maximum possible height of her plot.

Input

The first line contains two integers $n$ and $m$ ($1 \leq n, m \leq 8$), the number of rows and columns in the grid.

The following $n$ lines each contain a string of length $m$. This grid represents the information Torunn collected; each digit corresponds to the number of adjacent cells that have a lower height than the cell with that digit. It is guaranteed that there is at least one way to assign the heights $1, 2, \dots , n \cdot m$ to the cells such that the collected information is correct. Note that the values collected will always be between $0$ and $4$.

Output

Output two integers, the minimum and maximum possible height of the cell in the top-left corner.

Scoring

Your solution will be tested on a set of test groups, each worth a number of points. Each test group contains a set of test cases. To get the points for a test group you need to solve all test cases in the test group.

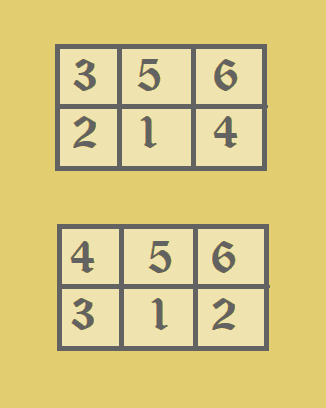
2 3
122
101

3 4

1 4
0111

1 1