Travar med böcker
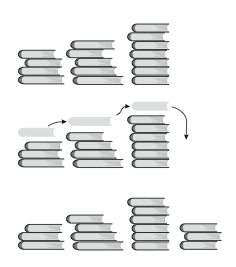
På ett bord ligger att antal travar med böcker. Varje dag tas en bok från varje trave. Dessa böcker bildar tillsammans en ny trave till höger om de andra, se figur 1. Om en trave blir tom skjuts travarna samman från höger. Eftersom det finns ett ändligt antal böcker, kommer förr eller senare samma upplägg att återkomma. Din uppgift blir nu att skriva ett program som frågar efter första uppläggets utseende och sedan tar reda på hur lång tid det tar innan ett upplägg som tidigare funnits, återkommer.
|
Dag |
Hög 1 |
Hög 2 |
Hög 3 |
Hög 4 |
Hög 5 |
Hög 6 |
|
1 |
4 |
5 |
7 |
|||
|
2 |
3 |
4 |
6 |
3 |
||
|
3 |
2 |
3 |
5 |
2 |
4 |
|
|
4 |
1 |
2 |
4 |
1 |
3 |
5 |
|
5 |
1 |
3 |
2 |
4 |
6 |
|
|
6 |
2 |
1 |
3 |
5 |
5 |
|
|
7 |
1 |
2 |
4 |
4 |
5 |
|
|
8 |
1 |
3 |
3 |
4 |
5 |
|
|
9 |
2 |
2 |
3 |
4 |
5 |
|
|
10 |
1 |
1 |
2 |
3 |
4 |
5 |
|
11 |
1 |
2 |
3 |
4 |
6 |
|
|
12 |
1 |
2 |
3 |
5 |
5 |
|
|
13 |
1 |
2 |
4 |
4 |
5 |
I tabellen ovan visas hur antalet böcker i travarna varierar under 13 dagar. I de kommande testerna är antalet böcker $ \le 50$, antalet travar som mest $ \le 15$ och antalet dagar $ \le 100$.
Indata
Första raden består av ett heltal - antalet boktravar $N$. Nästa rad består av $N$ heltal - antalet böcker i travarna
Utdata
Utdata ska bestå av två heltal - de två första dagarna där uppställningen upprepades. Den första dagen ska skrivas ut först.
| Sample Input 1 | Sample Output 1 |
|---|---|
3 4 5 7 |
7 13 |

