Problem I
Bikupor

Exempel $1$ till vänster, och exempel $2$ till höger.

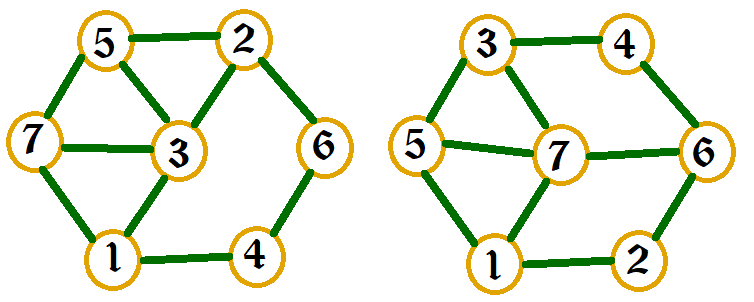
Biodlaren Bie har kommit fram till att hennes bin skulle må bra av att flytta ut i skogen. Därför har hon fått lov av gubben Ljungström att placera ut bikupor i hans skog. Ljungströms skog kan representeras av en oriktad graf med $N$ noder och $M$ kanter. Noderna är numrerade från $1$ till $N$. Först får Bie välja mellan $1$ och $N-K$ noder att placera ut sina bikupor på. Ljungström är dock också biodlare, och efter Bie har placerat ut sina kupor kommer Ljungström att placera ut sina egna! Bie vet att Ljungström alltid kommer ta de $K$ noder med högst nummer av de som hon inte valde. Eftersom Ljungströms bin är ovanligt aggressiva är det viktigt för Bie att se till så att ingen av hennes noder är närliggande (delar en kant) med någon av dessa noder.

Din uppgift är att hitta en mängd av högst $N-K$ noder sådan att om Ljungström väljer de $K$ återstående noderna med högst index, så hamnar ingen av dem bredvid någon av dem som du valde.

Indata

Den första raden innehåller tre heltal: $N$ ($2 \le N \le 2 \cdot 10^5$), $M$ ($1 \leq M \leq 4\cdot 10^5$), och $K$ ($1 \leq K \leq N-1$).

De följande $M$ raderna innehåller två heltal var: $u_ i$ och $v_ i$ ($1 \leq u_ i, v_ i \leq N$), vilket innebär att den $i$:te kanten kopplar samman noderna $u_ i$ och $v_ i$.

Grafen kommer inte innehålla kanter som går från en nod till sig själv, eller flera kanter som går mellan samma par av noder. Det är också garanterat att grafen är sammanhängande, dvs. det går att ta sig mellan varje par av noder genom att gå längs med kanterna.

Utdata

Om det inte finns någon giltig mängd av noder, skriv ut “-1”.

Annars, skriv först ut en rad med heltalet $L$, antalet noder i din mängd. Skriv därefter ut en rad med $L$ heltal $a_1, a_2, \dots , a_ L$, index på noderna du valde.

Om det finns flera lösningar kan du skriva ut vilken som helst.

Poängsättning

Din lösning kommer att testas på en mängd testfallsgrupper. För att få poäng för en grupp så måste du klara alla testfall i gruppen.

Exempelfall

7 10 3
3 1
3 7
3 5
3 2
1 7
7 5
5 2
2 6
6 4
4 1

2
4 6 

7 10 2
7 1
7 5
7 3
7 6
1 5
5 3
3 4
4 6
6 2
2 1

-1